The generalized fundamental law of active management
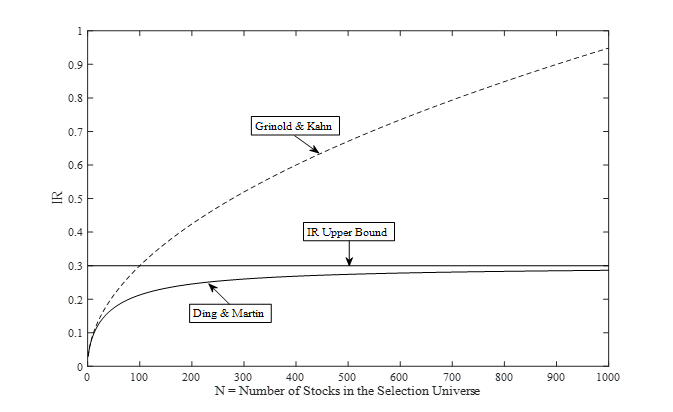
The generalized fundamental law of active management establishes the underlying relationship between expected portfolio performance (IR) and the portfolio characteristics based on bets on quantitative factors such as momentum, value, etc. It extends the work by Grinold and Kahn to the more interesting case where factor information coefficients (ICs) are time-varying.
Let’s say an investor wants to build a long-short dollar neutral portfolio by betting on stocks with high momentum, and shorting stocks with low momentum from a selection universe with N stocks, what will be her/his expected portfolio information ratio (IR)? The answer is the generalized fundamental law of active management:
![Rendered by QuickLaTeX.com \[ \text{IR} = \frac{{\mu}_{\text{IC}}}{\sqrt{(1-{\mu}_{\text{IC}}^2-{\sigma}_{\text{IC}}^2)/N+{\sigma}_{\text{IC}}^2}} \approx \frac{{\mu}_{\text{IC}}}{{\sigma}_{\text{IC}}} \]](https://alphafocusir.com/wp-content/ql-cache/quicklatex.com-eb47e1ccd14ac909d2cc9e2c33fd3f4d_l3.png)
where ![]() is the mean IC (Information Coefficient, correlation) between risk adjusted stock excess returns and risk adjusted factor exposures,
is the mean IC (Information Coefficient, correlation) between risk adjusted stock excess returns and risk adjusted factor exposures, ![]() is the IC standard deviation.
is the IC standard deviation.
Figure 1. The fundamental law of active management
![Rendered by QuickLaTeX.com \[ {\mathbf{w}_{A,t}} = {\frac{1}{N}} {\boldsymbol{\Lambda}}_t^{-1/2} {\mathbf{Z}}_{t-1}{\frac{{{\sigma}_A}{\boldsymbol{\Sigma}}_{\text{IC}}^{-1}{\boldsymbol{\mu}}_{\text{IC}}}{\sqrt{{{\boldsymbol {\mu}}_{\text{IC}}^'}{\boldsymbol{\Sigma}}_{\text{IC}}^{-1}{\boldsymbol{\mu}}_{\text{IC}}}}}} ={\frac{1}{N}} {\boldsymbol{\Lambda}}_t^{-1/2} {\mathbf{Z}}_{t-1}{\mathbf{w}_f}={\left({\frac{1}{N{\sigma}_{r_{it}}}}\sum_{k=1}^{K}{{w_{f,k}}{z_{ik,t-1}}}\right)}_{i=1,\ldots,N} \]](https://alphafocusir.com/wp-content/ql-cache/quicklatex.com-ac1cc58dd53c7c6a5b60531b727573a3_l3.png)
![Rendered by QuickLaTeX.com \[ {\mathbf{w}_f} = {\frac{{{\sigma}_A}{\boldsymbol{\Sigma}}_{\text{IC}}^{-1}{\boldsymbol{\mu}}_{\text{IC}}}{\sqrt{{{\boldsymbol {\mu}}_{\text{IC}}^'}{\boldsymbol{\Sigma}}_{\text{IC}}^{-1}{\boldsymbol{\mu}}_{\text{IC}}}}}} \]](https://alphafocusir.com/wp-content/ql-cache/quicklatex.com-a6b90cda11dc174d490486e8aae7db55_l3.png)
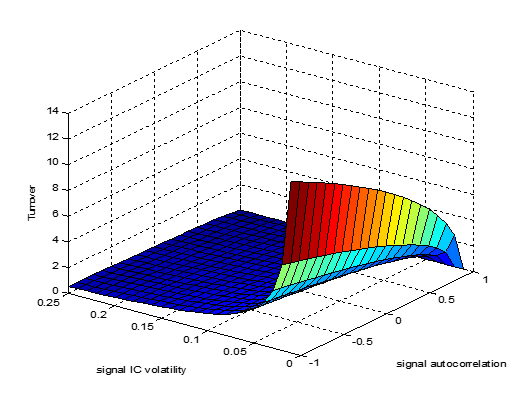
![Rendered by QuickLaTeX.com \[ \text{TO} = \frac{{\sigma}_A \sqrt{1-{\rho}_z}}{\sqrt{\pi} \sqrt{(1-{\mu}_{\text{IC}}^2-{\sigma}_{\text{IC}}^2)/N+{\sigma}_{\text{IC}}^2}} E_{cs}{\left(\frac{1}{{\sigma}_{r_i}}\right)} \]](https://alphafocusir.com/wp-content/ql-cache/quicklatex.com-4540ccfe7443ee802fbe4795404951c7_l3.png)